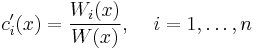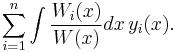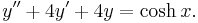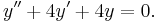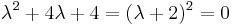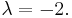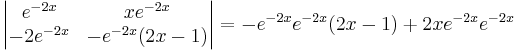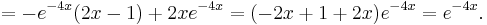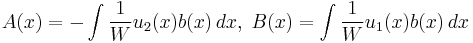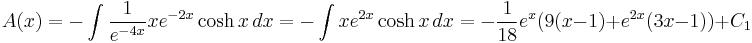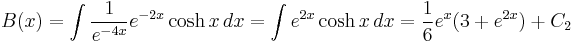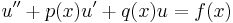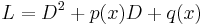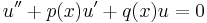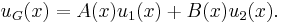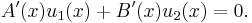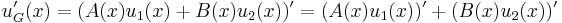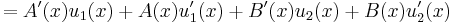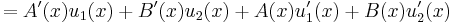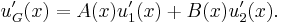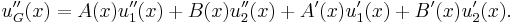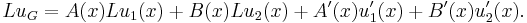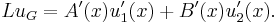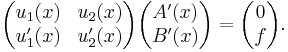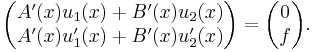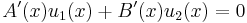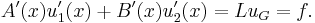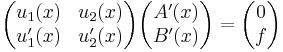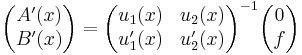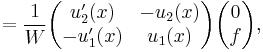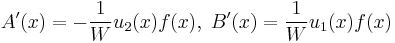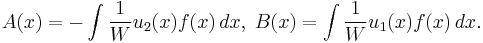Variation of parameters
In mathematics, variation of parameters, also known as variation of constants, is a general method to solve inhomogeneous linear ordinary differential equations. It was developed by Joseph Louis Lagrange.
For first-order inhomogeneous linear differential equations it is usually possible to find solutions via integrating factors or undetermined coefficients with considerably less effort, although those methods leverage heuristics that involve guessing and don't work for all inhomogenous linear differential equations.
Variation of parameters extends to linear partial differential equations as well, specifically to inhomogeneous problems for linear evolution equations like the heat equation, wave equation, and vibrating plate equation. In this setting, the method is more often known as Duhamel's principle, named after Jean-Marie Duhamel who first applied the method to solve the inhomogeneous heat equation. Sometimes variation of parameters itself is called Duhamel's principle and vice-versa.
Contents |
Description of method
Given an ordinary non-homogeneous linear differential equation of order n
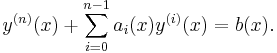 (i)
(i)
let  be a fundamental system of the corresponding homogeneous equation
be a fundamental system of the corresponding homogeneous equation
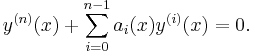 (ii)
(ii)
Then a particular solution to the non-homogeneous equation is given by
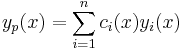 (iii)
(iii)
where the 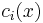 are continuous functions which satisfy the equations
are continuous functions which satisfy the equations
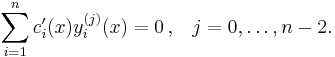 (iv)
(iv)
By substituting (iii) into (i) and applying (iv) it follows that
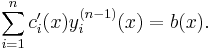 (v)
(v)
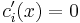 for all x and i is the only way to satisfy the condition, since all
for all x and i is the only way to satisfy the condition, since all 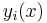 are linearly independent. It implies that all
are linearly independent. It implies that all 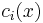 are independent of x in the homogeneous case b(x)=0. )
are independent of x in the homogeneous case b(x)=0. )
This linear system of n equations can then be solved using Cramer's rule yielding
where 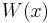 is the Wronskian determinant of the fundamental system and
is the Wronskian determinant of the fundamental system and 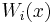 is the Wronskian determinant of the fundamental system with the i-th column replaced by
is the Wronskian determinant of the fundamental system with the i-th column replaced by 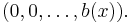
The particular solution to the non-homogeneous equation can then be written as
Examples
Specific second order equation
Let us solve
We want to find the general solution to the differential equation, that is, we want to find solutions to the homogeneous differential equation
From the characteristic equation
Since we have a repeated root, we have to introduce a factor of x for one solution to ensure linear independence.
So, we obtain u1 = e−2x, and u2 = xe−2x. The Wronskian of these two functions is
Because the Wronskian is non-zero, the two functions are linearly independent, so this is in fact the general solution for the homogeneous differential equation (and not a mere subset of it).
We seek functions A(x) and B(x) so A(x)u1 + B(x)u2 is a general solution of the non-homogeneous equation. We need only calculate the integrals
that is,
where 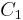 and
and 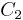 are constants of integration.
are constants of integration.
General second order equation
We have a differential equation of the form
and we define the linear operator
where D represents the differential operator. We therefore have to solve the equation 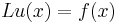 for
for 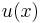 , where
, where  and
and  are known.
are known.
We must solve first the corresponding homogeneous equation:
by the technique of our choice. Once we've obtained two linearly independent solutions to this homogeneous differential equation (because this ODE is second-order) — call them u1 and u2 — we can proceed with variation of parameters.
Now, we seek the general solution to the differential equation 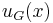 which we assume to be of the form
which we assume to be of the form
Here, 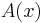 and
and 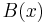 are unknown and
are unknown and 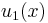 and
and 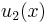 are the solutions to the homogeneous equation. Observe that if
are the solutions to the homogeneous equation. Observe that if 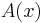 and
and 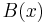 are constants, then
are constants, then 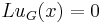 . We desire A=A(x) and B=B(x) to be of the form
. We desire A=A(x) and B=B(x) to be of the form
Now,
and since we have required the above condition, then we have
Differentiating again (omitting intermediary steps)
Now we can write the action of L upon uG as
Since u1 and u2 are solutions, then
We have the system of equations
Expanding,
So the above system determines precisely the conditions
We seek A(x) and B(x) from these conditions, so, given
we can solve for (A′(x), B′(x))T, so
where W denotes the Wronskian of u1 and u2. (We know that W is nonzero, from the assumption that u1 and u2 are linearly independent.)
So,
While homogeneous equations are relatively easy to solve, this method allows the calculation of the coefficients of the general solution of the inhomogeneous equation, and thus the complete general solution of the inhomogeneous equation can be determined.
Note that 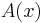 and
and 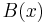 are each determined only up to an arbitrary additive constant (the constant of integration); one would expect two constants of integration because the original equation was second order. Adding a constant to
are each determined only up to an arbitrary additive constant (the constant of integration); one would expect two constants of integration because the original equation was second order. Adding a constant to 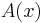 or
or 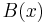 does not change the value of
does not change the value of 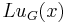 because
because  is linear.
is linear.
References
- Coddington, Earl A.; Levinson, Norman (1955). Theory of Ordinary Differential Equations. New York: McGraw-Hill.
- Boyce, W. E.; DiPrima, R. C. (1965). Elementary Differential Equations and Boundary Value Problems 8th Edition. Wiley Interscience., pages 186-192, 237-241
- Teschl, Gerald. Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. http://www.mat.univie.ac.at/~gerald/ftp/book-ode/.